Simplestar Game
since 17/01/2009
:::::::::::039話 いろいろな衝突形状:::::::::::
Bullet の衝突判定について学んだ 前回 に引き続き
今回は様々な衝突形状の登録の仕方について学んでみたいと思います。
いろいろな衝突形状を扱えるようになると、衝突判定がおもしろくなってくると思います。
今回のイラストはペンタブから描いてみたんですよ…はい、本題に戻ります。
衝突判定を行ったとき、衝突形状はほとんどボックス（立方体または直方体）でしたね。
bullet で扱える衝突物体はこれだけではありません。
それでは、どれくらいのものがあるのか見ていきましょう。
ひとまず、ドキュメントに書かれているものを以下に列挙してみます。
btBoxShape : ボックス（XYZ軸方向の一辺の半分の長さを指定して作成）
btSphereShape : 球体（半径の長さを指定して作成）
btCapsuleShape: カプセル（Y軸方向に伸びた）、X, Z 方向なら btCapsuleShapeX/Z を使いましょう。
btCylinderShape : 円柱（Y軸方向に伸びた）、X, Z 方向なら btCylinderShapeX/Z を使いましょう。
btConeShape : コーン（Y軸方向に伸びた）、X, Z 方向なら btConeShapeX/Z を使いましょう。
btMultiSphereShape : 複数の球体で表現する衝突形状。（例：2個の球体を使えばカプセルになる。）
btTriangleShapeEx : 通常の環境では使えないのかな？クラスが定義されていませんでした。
（btTriangleMeshShape, btConvexTriangleMeshShape の三角形一個版で代用できます。）
btConvexTriangleMeshShape : 外接頂点で構成される多角体。 メッシュ情報から作ります。（かなり低速らしい…）
btConvexPointCloudShape : 通常の環境では使えないのかな？クラスが定義されていませんでした。
意味合い的に btConvexHullShape で代用可能です。
btConvexHullShape : 外接頂点で構成される多角体。頂点バッファから作ります。
（btConvexTriangleMeshShape を使うなら、より高速なこっちを使いましょう。）
btTetrahedronShapeEx : 通常の環境では使えないのかな？クラスが定義されていませんでした。
btSoftClusterCollisionShape : 通常の環境では使えないのかな？クラスが定義されていませんでした。
bMinkowskiSumShape : ミンコフスキー統合体和。上級者向けらしいが、資料不足のため確認方法から不明…（追記：きっと内部で衝突判定に使っているはず）
btUniformScalingShape : 上記のシェイプを拡大または縮小したもの。
以下は上記の Convex (凸形状) と異なり Concave (凹形状) を表現する場合に用います。
btBvhTriangleMeshShape : 三角形メッシュです。btConvexTriangleMeshShapeと大きく違う点は凹形状を表現できる点です。
btMultimaterialTriangleMeshShape : 面ごとにマテリアルがついた三角形メッシュです。
btStaticPlaneShape : 世界を二分する無限平面。mass を 0 にして使いますが、0 にしない場合は押し進められます。
btPlaneShape : クラスが定義されていませんでした。（単独では使えないのかな？）
btSoftBodyCollisionShape :（勉強中）ソフトボディをもう少し学んでから更新します。
btScaledBvhTriangleMeshShape : 三角形メッシュをXYZ軸でスケーリングして使用できます。
btHeightfieldTerrainShape : 格子状にメッシュが切られていて、それぞれの頂点の高さを指定できます。（高さフィールド）
btEmptyShape :（勉強中）
btGImpactMeshShape : 通常の環境では使えないのかな？クラスが定義されていませんでした。
btGImpactMeshShapePart : 通常の環境では使えないのかな？クラスが定義されていませんでした。
btGImpactCompoundMeshShape : 通常の環境では使えないのかな？クラスが定義されていませんでした。
btCompoundShape : すべての衝突形状を連結、統合して一つの衝突形状を作成します。
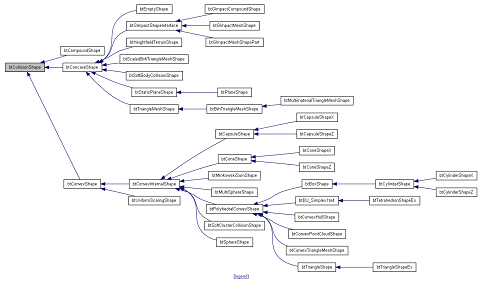
クラスの関係図は次に示す通りです、一通り確認していきましょう。
※クリックで拡大
さて、これらを world へ登録する方法を順番に見ていくとして、最終的にどの形状も扱えるようになったとします。
そのとき最もパフォーマンスが出て、品質が高いシミュレーション結果を得るためには、どうすれば良いのか？
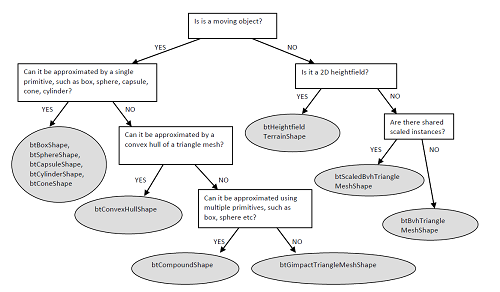
そんな疑問が出てきたら次の選択表を参考に衝突形状を決定してみてはいかがでしょうか？
※クリックで拡大
質問が深くなるにつれて、衝突形状の精度は上がっていきます。
ただし、パフォーマンスは落ちていくというイメージを持っておきましょう。
btBoxShape
ボックスです。
XYZ軸方向の辺の半分の長さ[m]を指定して形状を作成します。
1 | btCollisionShape* pColShape = new btBoxShape(btVector3(1,1,1)); |
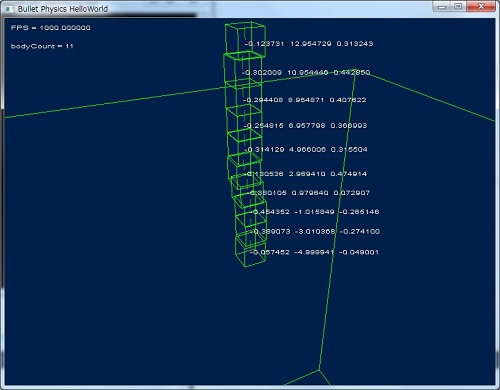
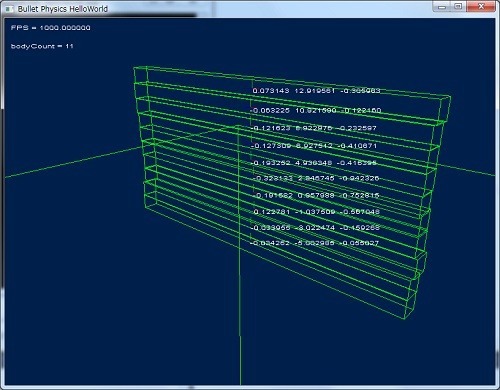
DebugView で描画した場合の結果
確認は簡単にできます。
長方形とか試してみました。↓
1 | btCollisionShape* pColShape = new btBoxShape(btVector3(20,1,1)); |
btSphereShape
球体です。
半径の長さ[m]を指定して形状を作成します。
1 | btCollisionShape* pColShape = new btSphereShape(btScalar(3.)); |
DebugView で描画した場合の結果
ディフォルトの DebugView の場合、球体はダイアモンドで描画されます。
半径以外に指定するものはありませんし、特に説明は必要ないですね。
btCapsuleShape
カプセルです。
第1引数に球体部分の半径の長さ[m]を指定し
第2引数に円柱部分の高さ[m]を指定します。
1 | btCollisionShape* pColShape = new btCapsuleShape(btScalar(2.), btScalar(3.)); |
DebugView で描画した場合の結果
ディフォルトの DebugView の場合、球体は部分はダイアモンドで描画され、円柱部分はひし形になります。
btMultiSphereShape の球体2つバージョンとも呼べるそうです。
btCapsuleShapeX, btCapsuleShapeZ についても試してみました
それぞれ円柱部分が指定した軸に沿うようになります。
btCylinderShape
円柱です。（シリンダー）
btVector3 をコンストラクタに渡すのですが
X値に底面の円の半径の長さ[m]を指定し
Y値に円柱の高さ[m]を指定します。
Z値には底面の円の半径と同じ値を指定しないといけないようです。
（すみませんドキュメントに詳細が無く、ソースコードにもコメントが無いので想像です。）
とにかく値を小さくすると（0を指定とか）、良く跳ねます。（まるでゴムタイヤのようでした。）
大きい値にすると(100を指定とか)、跳ねなくなります。（まるでドラム缶のようになります。）
試しに -10 とか指定したら、側面に他の衝突物体がめり込み、その後無限に跳ね続けました。
1 | btCollisionShape* pColShape = new btCylinderShape(btVector3(4.,2.,4.)); |
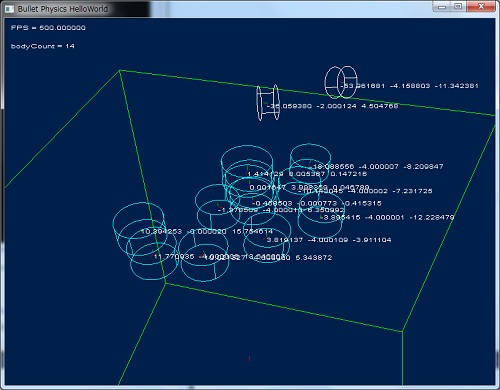
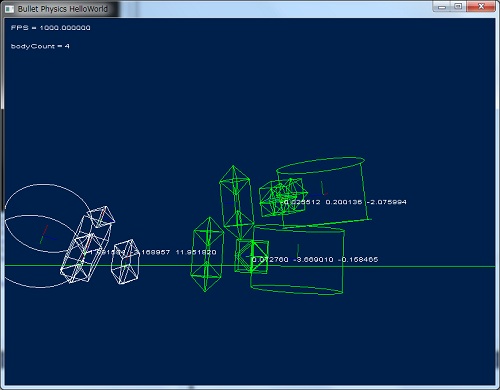
DebugView で描画した場合の結果
ディフォルトの DebugView の場合、底面と上面は円として描かれます。
側面はただの2つのラインが引かれるだけでした。
コンストラクタで渡す btVector3 の Z値が何なのか本当に気になるのだけど…。
（公式のドキュメントはどこだ！）
btCylinderShapeX, btCylinderShapeZ について試したところ、なんということでしょう！
たとえば ShapeX の方はコンストラクタで渡す btVector3 の X値が円柱の高さになり
Y値が底面の円の半径になりました。相変わらず Z値が妙なパラメータのようです。
しかし ShapeZ の方はコンストラクタで渡す btVector3 の Z値が円柱の高さになり
X値が底面の円の半径になりました。今度はY値が妙なパラメータでした。
また、面白いことにおかしな動きをする境は底面の円の半径よりも、問題となっている残りの成分が大きいか小さいか
にあるようでした。（小さい場合に、ぴょんぴょん跳ねます。なんなんでしょうね…）
それと、それぞれ円柱部分が指定した軸に沿うようになるのはカプセルのときと一緒でした。
btConeShape
コーンです。
第1引数に底面の円の半径の長さ[m]を指定し
第2引数にコーンの高さ[m]を指定します。
1 | btCollisionShape* pColShape = new btConeShape(btScalar(2.), btScalar(3.)); |
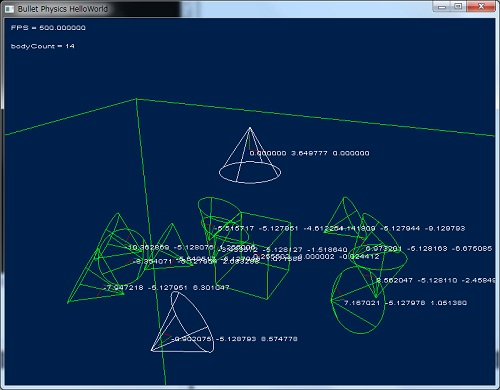
DebugView で描画した場合の結果
ディフォルトの DebugView の場合、底面は円で描かれ、側面にはスリットが4本入っています。
btMultiSphereShape の球体2つバージョンとも呼べるそうです。
btConeShapeX, btConeShapeZ についても試してみました。
それぞれコーンの示す方向が指定した軸に沿うようになります。
btMultiSphereShape
複数の球体で構成される衝突形状です。
ローカル位置配列と、それぞれの球の半径の配列を指定して作成します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | const int numSpheres = 3;btVector3 psitions[numSpheres];{ psitions[0] = btVector3(-3.,0.,0.); psitions[1] = btVector3(0.,0.,0.); psitions[2] = btVector3(3.,0.,0.);}btScalar radi[numSpheres];{ radi[0] = btScalar(1.); radi[1] = btScalar(2.); radi[2] = btScalar(1.);}btCollisionShape* pColShape = new btMultiSphereShape(psitions, radi, numSpheres); |
DebugView で描画した場合の結果
ディフォルトの DebugView の場合、球体はダイアモンドで描画されます。
砂時計の形など、くびれをもたせるようなことはできないようです。
たとえば2つの球ではカプセル型しか作れません。
※ただし、片方の球体が大きいなど、特殊なカプセルは作成できます。
btConvexTriangleMeshShape
頂点バッファとインデックスバッファより作成する、外接頂点で構成される多角体です。
台形など、ちょっとだけ複雑な積み木の部品などを表現しやすいです。
btConvexHullShape の方が比較的高速なので、基本はそっちを使った方が良いですが
どうしてもメッシュデータからそのまま作成した場合はこちらで作ります。
以下のインデックスバッファのトポロジは三角形ストリップであることに注意してください。
トポロジを三角形リストにしたい場合は、インデックス数を三角形の数 x3 にすれば勝手に対応してくれます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | static int triangleIndices[] = {0,1,2,3,4,5,6,7};static btVector3 triangleVertices[] = { btVector3(-3.,-1.,1.), btVector3(-3.,-1.,-1.), btVector3(-1.,1.,1.), btVector3(-1.,1.,-1.), btVector3(1.,1.,1.), btVector3(1.,1.,-1.), btVector3(3.,-1.,1.), btVector3(3.,-1.,-1.)};const int numTriangles = 6; int* pTriangleIndexBase = triangleIndices; const int triangleIndexStride = sizeof(int); const int numVertices = 8; btScalar * pVertexBase = (btScalar*)triangleVertices;const int vertexStride = sizeof(btVector3); btStridingMeshInterface* pMeshData = new btTriangleIndexVertexArray( numTriangles, pTriangleIndexBase, triangleIndexStride, numVertices, pVertexBase, vertexStride ); btCollisionShape* pColShape = new btConvexTriangleMeshShape(pMeshData, true); |
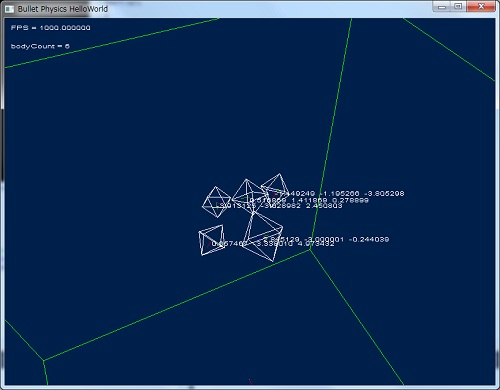
DebugView で描画した場合の結果
※頂点バッファとインデックスバッファは利用している最中に壊してはいけません。
static で配列を作っているのはそれが理由ですが、利用するときは十分注意してください。
btConvexHullShape
頂点バッファより作成する、外接頂点で構成される多角体です。
台形など、ちょっとだけ複雑な積み木の部品などを表現しやすいです。
btConvexTriangleMeshShape と比べて高速です。
また addPoint 関数で後から頂点を追加できるので便利です！
1 2 3 4 5 6 7 8 9 10 | const int numPoints = 9;btVector3 points[] = { btVector3(1.,0.,1.), btVector3(1.,0.,-1.), btVector3(-1.,0.,1.), btVector3(-1.,0.,-1.), btVector3(1.,-2.,-1.), btVector3(1.,-2.,1.), btVector3(-1.,-2.,-1.), btVector3(-1.,-2.,1.), btVector3(0.,2.,0.)};const int pointStride = sizeof(btVector3);btConvexHullShape* pConvexHullShape = new btConvexHullShape( (btScalar*)points, numPoints, pointStride );pConvexHullShape->addPoint(btVector3(0.,4.,0.));btCollisionShape* pColShape = pConvexHullShape; |
DebugView で描画した場合の結果
頂点バッファは利用している最中に壊しても大丈夫です。
btUniformScalingShape
これまで作成方法を見てきた btConvexShape を拡大縮小して再利用する場合に使います。
作り方は簡単、既に作成されている形状に、拡大縮小の係数を掛けるだけです。
1 2 3 4 5 6 7 8 9 10 11 | const int numPoints = 9;btVector3 points[] = { btVector3(1.,0.,1.), btVector3(1.,0.,-1.), btVector3(-1.,0.,1.), btVector3(-1.,0.,-1.), btVector3(1.,-2.,-1.), btVector3(1.,-2.,1.), btVector3(-1.,-2.,-1.), btVector3(-1.,-2.,1.), btVector3(0.,2.,0.)};const int pointStride = sizeof(btVector3);btConvexHullShape* pConvexHullShape = new btConvexHullShape( (btScalar*)points, numPoints, pointStride );pConvexHullShape->addPoint(btVector3(0.,4.,0.));btCollisionShape* pColShape = new btUniformScalingShape(pConvexHullShape, btScalar(0.5)); |
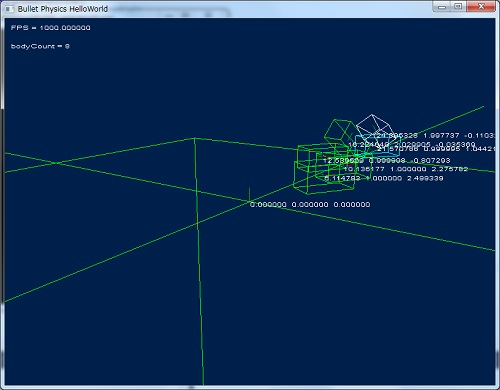
DebugView で描画した場合の結果
DebugView では何も表示されないようです。
ただし、しっかり拡大縮小した形状の当たり判定は行えているようでした。
btBvhTriangleMeshShape
最も一般的な凹形状の衝突形状の作成方法です。
利点はモデリングソフトから出力したデータなどの
頂点バッファとインデックスバッファから作成できる点ですね。
以下の作成例はトポロジに三角形ストリップを使っていますが、三角形リストでも作れます。
その場合はインデックス数が三角形数 x3 になっていれば勝手に対応してくれます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | static int triangleIndices[] = {0,1,2,3,4,5,6,7};static btVector3 triangleVertices[] = { btVector3(-3.,-1.,1.), btVector3(-3.,-1.,-1.), btVector3(-1.,1.,1.), btVector3(-1.,1.,-1.), btVector3(1.,1.,1.), btVector3(1.,1.,-1.), btVector3(3.,-1.,1.), btVector3(3.,-1.,-1.)};const int numTriangles = 6; int* pTriangleIndexBase = triangleIndices; const int triangleIndexStride = sizeof(int); const int numVertices = 8; btScalar * pVertexBase = (btScalar*)triangleVertices;const int vertexStride = sizeof(btVector3); btStridingMeshInterface* pMeshData = new btTriangleIndexVertexArray( numTriangles, pTriangleIndexBase, triangleIndexStride, numVertices, pVertexBase, vertexStride );btCollisionShape* pColShape = new btBvhTriangleMeshShape(pMeshData, true); |
DebugView で描画した場合の結果
メッシュのくぼんでいる部分も当たり判定が有効になります。（ただしパフォーマンスはガタ落ちします。）
※インデックスバッファと頂点バッファを使用中に壊さないよう注意してご使用ください。
バッファの作成とシェイプの用意についてですが、最適化してデータを用意しています。
平坦なメッシュが続くとそれを一つの形状に統合しておくなどですが…（おそらく）
あらかじめ計算して作ったデータをディスクに保存しておき、利用するときにそのファイルから
衝突形状を作成する方法があります。（これにより計算をスキップでき、準備時間を短縮できます。）
このシリアライズと呼ばれるこの方法、次のようにして実装します。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | btBvhTriangleMeshShape* pTriMeshShape = new btBvhTriangleMeshShape(pMeshData, true); const int maxSerializeBufferSize = 1024*1024*5; btDefaultSerializer* serializer = new btDefaultSerializer(maxSerializeBufferSize); serializer->startSerialization(); #ifdef SERIALIZE_SHAPE pTriMeshShape->serializeSingleShape(serializer);#else pTriMeshShape->serializeSingleBvh(serializer);#endif serializer->finishSerialization(); FILE* f2 = fopen("myShape.bullet","wb"); fwrite(serializer->getBufferPointer(),serializer->getCurrentBufferSize(),1,f2); fclose(f2); |
シリアライズしたファイルから、最適化したメッシュ衝突形状を作成するには次のように書きます。
この処理をデシリアライズと呼びます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | btBvhTriangleMeshShape* pTriMeshShape = 0;btBulletWorldImporter import(0);//don't store info into the worldif (import.loadFile("myShape.bullet")){ int numBvh = import.getNumBvhs(); int numShape = import.getNumCollisionShapes(); if (numBvh) { btOptimizedBvh* bvh = import.getBvhByIndex(0); bool bBuildBvh = false; pTriMeshShape = new btBvhTriangleMeshShape(pMeshData, true, bBuildBvh); pTriMeshShape->setOptimizedBvh(bvh); } else if (numShape) { pTriMeshShape = (btBvhTriangleMeshShape*)import.getCollisionShapeByIndex(0); //if you know the name, you can also try to get the shape by name: const char* meshName = import.getNameForPointer(pTriMeshShape); if (meshName) { pTriMeshShape = (btBvhTriangleMeshShape*)import.getCollisionShapeByName(meshName); } }} |
デシリアライズで使用している btBulletWorldImporter ですが、これは Bullet を展開したフォルダの
Extras\Serialize\BulletWorldImporter 以下のヘッダファイルとソースファイルで定義されています。
利用する際はこのヘッダファイルとソースファイルを組み込んでお使いください。
このシリアライズとデシリアライズの話ですが、他とは違い資料が豊富でわかりやすかったです。
Demo の ConcaveDemo を是非参考にしてください。
btMultimaterialTriangleMeshShape
作り方は上記の三角形メッシュに似ています。
違う点と言えば
コンストラクタで渡すのが頂点バッファ、インデックスバッファのほかにマテリアルバッファ
を含んだ btTriangleIndexVertexMaterialArray クラスになります。
マテリアルがどんなものかは自分で決められるようで、衝突時にコールバックでも用意しておけば
対象をアップキャストしてそこからマテリアルを取り出せるようになる感じです。
ゴルフゲームとか、よく使う場面がありそうなイメージですが
資料が少ないため、実装の詳細は想像するしかないです。
また今度、詳細がわかったら更新します。
btStaticPlaneShape
世界を分断する無限平面です。
mass を 0 に設定して使います。
mass が 0 でない場合、その無限平面を押し進めることが可能のようです。
（なかなか面白い…）
作成コードは次の通り。
第1引数は面の法線、第2引数は壁の厚さを表します。
1 | btCollisionShape* pColShape = new btStaticPlaneShape(btVector3(0.,1.,0.), btScalar(0.)); |
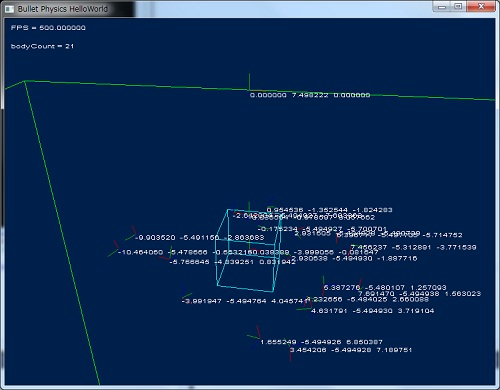
DebugView で描画した場合の結果
startTransform.setOrigin 関数で配置します。
btRigidBodyConstructionInfo で渡す mass の値は 0 であること。
これを忘れると、面が移動してしまうので注意が必要です。
btScaledBvhTriangleMeshShape
三角形メッシュを拡大したり縮小したりして使用できます。
作成コードは次の通り。
第1引数は作成済みの btBvhTriangleMeshShape のポインタ、第2引数はXYZ軸の拡大縮小の係数です。
1 | btCollisionShape* pColShape = new btScaledBvhTriangleMeshShape(pTriMeshShape, btVector3(1.,3.,1.)); |
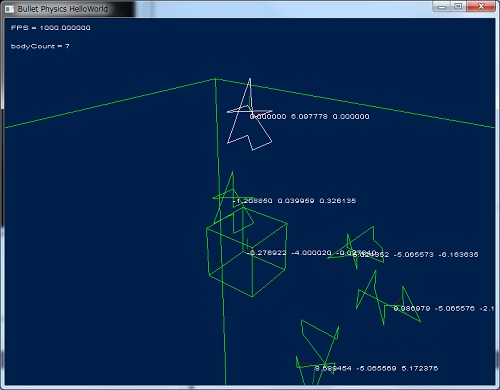
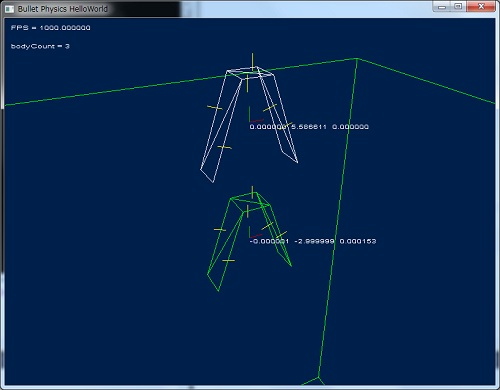
DebugView で描画した場合の結果
ちょっと関係ない話かもしれませんが、一つ上の btStaticPlaneShape とは衝突しない模様。
スルーしていたのがバグなのか仕様なのか、わかりませんがここにメモしておきます。
btHeightfieldTerrainShape
格子状にメッシュが切られていて、それぞれの頂点の高さを指定すると
その地形のメッシュが出来上がります。
作成コードは次の通り。
メッシュを切る数と、高さ配列を渡すだけです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | btScalar maxHeight = 1.f;bool useFloatDatam=false;bool flipQuadEdges=false;int width=20;int length=20;unsigned char* heightfieldData = new unsigned char[width*length];{ for (int i=0;i<width*length;i++) { heightfieldData[i]=0; }}btHeightfieldTerrainShape* heightFieldShape = new btHeightfieldTerrainShape(width, length, heightfieldData, maxHeight, 1, useFloatDatam, flipQuadEdges); |
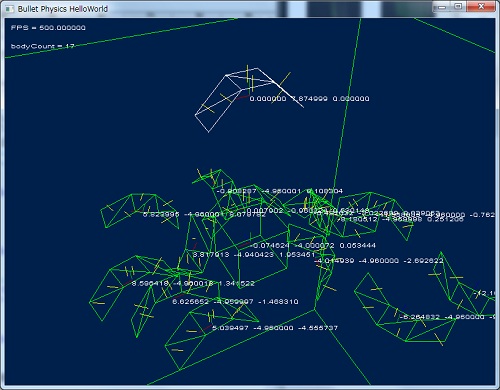
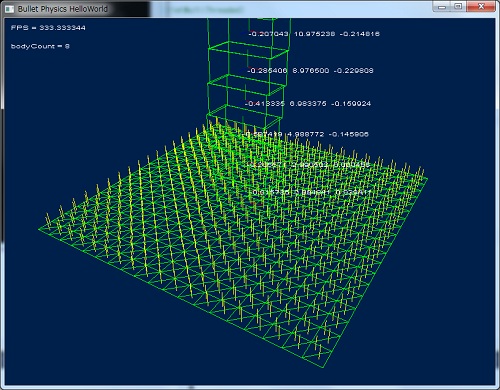
DebugView で描画した場合の結果
一見高速に動作しそうですが、ものすごい負荷がかかっていました。
フィールドとして利用するのはあまり現実的ではないかもしれません。
ちょっと関係ない話かもしれませんが、一つ上の btScaledBvhTriangleMeshShape とは衝突しない模様。
スルーしていたのがバグなのか仕様なのか、わかりませんがここにメモしておきます。
btCompoundShape
すべての衝突形状を連結、統合して一つの衝突形状にできます。
これまで見てきた形状すべてをつなぎ合わせることができるんです。素晴らしいです。
凹形状表現なので、くぼみや隙間に差し込むことができます。
作成コードは次の通り。
それぞれのシェイプの配置行列とともに追加していくだけです。
簡単ですね。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | btCompoundShape* pCompoundShape = new btCompoundShape();btTransform addTransform;addTransform.setIdentity();addTransform.setOrigin(btVector3(0.,0.,0.));pCompoundShape->addChildShape( addTransform, pBoxShape);addTransform.setOrigin(btVector3(3.,0.,0.));pCompoundShape->addChildShape( addTransform, pSphereShape);addTransform.setOrigin(btVector3(0.,0.,3.));pCompoundShape->addChildShape( addTransform, pCapsuleShape);addTransform.setOrigin(btVector3(-1.,0.,0.));pCompoundShape->addChildShape( addTransform, pCapsuleXShape);addTransform.setOrigin(btVector3(0.,0.,-3.));pCompoundShape->addChildShape( addTransform, pChylinderShape);btCollisionShape* pColShape = pCompoundShape; |
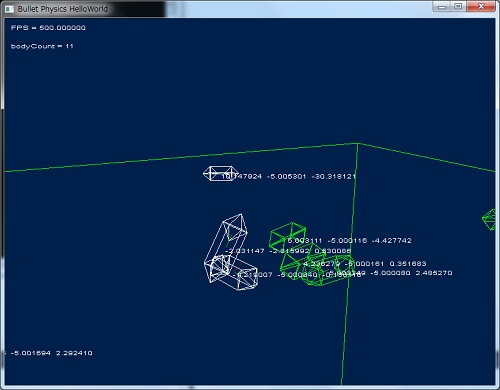
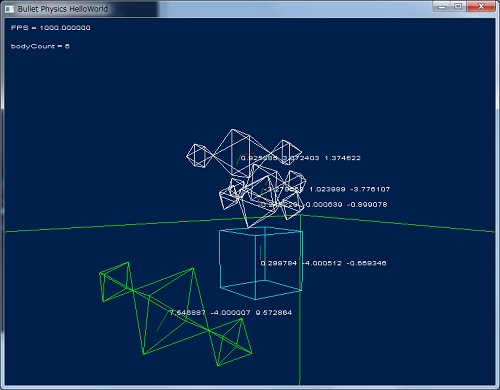
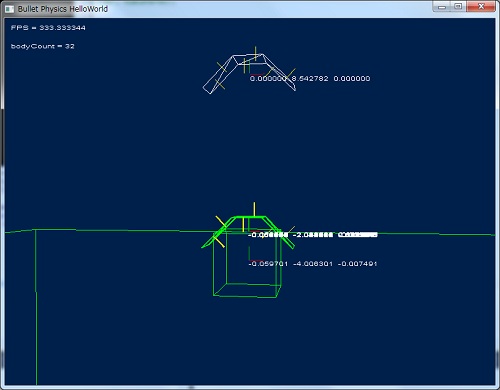
DebugView で描画した場合の結果
中央、くぼんだ部分にカプセルが入っているのが確認できます。
まとめ
いかがでしたでしょうか？
衝突判定に続き、今回は衝突形状の作り方について学びました。
一般的な使い方をする限りでは、ここで説明されたものだけで、十分かとおもいます。
今回の情報はドキュメントとリファレンスを読めば調べがつきますが
あとで自分が読み返して
こんな衝突形状があったなぁと思える一覧表の役割を果すことを期待します。
次回は、物体を拘束したり、動きに制約を与えたりする方法について学びます。
お楽しみに！
質疑応答
いくつか調べたので補足です。Gimpactほにゃららというやつですが、ココの衝突判定ライブラリを使用する場合に有効なもののようです。
あとミンコフスキー統合体ですが、多分ミンコフスキー和のことだと思います。Bulletの衝突判定アルゴリズムで内部的に利用している（はず）です。 by 名前がありません
情報提供ありがとうございます。
利用が確認できていない衝突形状について理解が深まりました。
当時ミンコフスキー統合体と書いたのは、SumできるMinkowskiというものでもあるのかな？と勝手に名前からイメージしてしまったためでした。
ミンコフスキー和、差とは、形状同士を足したり、引いたりしてできる形状のことで
このミンコフスキー差が原点を含むと形状同士が衝突していることがわかるという、衝突判定に用いる理論なのだなと理解してます。
（ミンコフスキーとはアインシュタインの先生の名前なんですね）
2011/09/03 初記。
2011/09/05 更新。
2014/10/26 更新。
